Geometrie des Menschen - Fibonacci-Spirale, Fibonacci-Sequenz

|
Zur Konstruktion eines Rechtecks in den
Proportionen des goldenen Schnittes aus
einem Quadrat teilt man dieses vertikal in der
Mitte und schlägt mit der Diagonalen des
Rechtecks als Radius einen Kreisbogen zur
Basis-Linie.
|
|
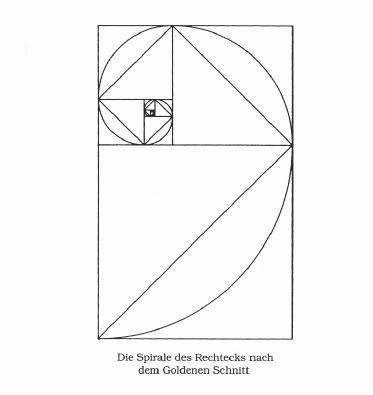
Im Rechteck des goldenen Schnittes kann
man nun mit dem Maß seiner kürzesten Kante
ein Quadrat zeichnen und einen Kreisbogen
darin mit dieser Kante als Radius.
Dabei entsteht ein weiteres kleineres Rechteck,
das wiederum in den Proportionen von
Phi=1,6180339... zum größeren Rechteck steht.
|

|
Leonardo Fibonacci (1180-1250), italienischer
Mathematiker, erkannte als erster den gesetz-
mäßigen Ablauf im Wachstums der Pflanzen
und in anderen biologischen Bereichen.
|

|
Geometrischer Vergleich zwischen
Rechteck des goldenen Schnitts links
+ Fibonacci-Rechteck rechts.
|
Beispiele zur Spirale des goldenen Schnittes :
Pyramiden von Gizeh + Spirale des goldenen Schnittes
Stern-Bild Orion + Spirale des goldenen Schnittes
Link: Phi und goldener Schnitt (in Englisch)
11 -> next -> last -> back